Lecture 19 Mar 19

Last time, we discussed:

• multiparticle states, e.g. \(\ket{\uparrow\downarrow}\) describes a state in which particle 1 is in a spin-up state and particle 2 is spin-down

• The particle exchange operator \(\hat{P}_{12}\), which switches the two particle labels, e.g. \(\hat{P}_{12}\ket{\uparrow\downarrow} = \ket{\downarrow\uparrow}\), ie. returns a state in which particle 1 is now in a spin-down state and particle 2 is spin-up.

• Because we have indistinguishable particles in quantum mechanics, the allowed multiparticle states are either symmetric or antisymmetric under the exchange of any two particle labels. For two spin-1/2 particles, the symmetric states are \(\ket{\uparrow\uparrow}\), \((\ket{\uparrow\downarrow}+\ket{\downarrow\uparrow})/\sqrt{2}\) and \(\ket{\downarrow\downarrow}\) and the antisymmetric state is \((\ket{\uparrow\downarrow}-\ket{\downarrow\uparrow})/\sqrt{2}\). You may recognize these states from the quantum 1 course: the symmetric states correspond to the eigenstates of total spin \(\hat{S} =\hat{S}_1 + \hat{S}_2\) with \(s=1\) (triplet states, \(m_s=-1,0,+1\)), whereas the antisymmetric state has \(s=0\) (singlet state, \(m_s=0\)).

• The spin-statistics theorem tells us that identical fermions have antisymmetric states with respect to particle interchange, whereas bosons have symmetric states.

Today we’ll apply these ideas to the helium atom.

Helium atom

The Hamiltonian for the helium atom is

\[\hat{H} = {\hat{p}_1^2\over 2m_e} + {\hat{p}_2^2\over 2m_e} - {Ze^2\over 4\pi \epsilon_0 r_1} - {Ze^2\over 4\pi \epsilon_0 r_2} + {e^2\over 4\pi \epsilon_0 |\mathbf{r}_2-\mathbf{r}_1|}\]

where we identify the position and momentum of each electron with subscripts \(1\) and \(2\) respectively, and \(Z=2\) is the number of protons in the nucleus. We’ve also ignored any motion of the nucleus (so we use \(m_e\) in the denominator of the kinetic energy terms rather than the reduced mass). We see that the Hamiltonian can be written as

\[\hat{H} = \hat{H}_1 + \hat{H}_2 + \hat{H}_\mathrm{int}\]

where \(\hat{H}_1\) and \(\hat{H}_2\) are two copies of the Hamiltonian for hydrogen-like atoms and

\[H_\mathrm{int} = {e^2\over 4\pi \epsilon_0 |\mathbf{r}_2-\mathbf{r}_1|}\]

represents the Coulomb repulsion between the two electrons.

This problem doesn’t have exact analytic solutions, but there are two approaches we can use to find approximate solutions. The first is to treat the interaction term in the Hamiltonian as a perturbation and use perturbation theory. The second is the variational method, in which we guess the ground state wavefunction and use it to derive an upper limit on the ground state energy.

Perturbation theory approach

If we ignore the Coulomb repulsion between the electrons (i.e. set \(\hat{H}_\mathrm{int}=0\)), we can construct stationary states using the one-electron states \(\psi_{n\ell m}(\mathbf{r})\ket{\uparrow}\) or \(\psi_{n\ell m}(\mathbf{r})\ket{\downarrow}\) for each electron. Because we are dealing with two identical fermions, we need to make the state antisymmetric with respect to particle interchange.

Ground state. Consider first the ground state. To get the lowest energy, we can put each electron into the \(n=1\) state, ie.

\[\psi(\mathbf{r}_1,\mathbf{r}_2) \propto \psi_{100}(\mathbf{r}_1)\psi_{100}(\mathbf{r}_2)\]

with a corresponding energy \(E = -2\times Z^2\times 13.6\ \mathrm{eV} = 108.8\ \mathrm{eV}\). Since the spatial part is symmetric with respect to particle interchange, we need the spin part to be antisymmetric, so there is only one choice – singlet – for the spin state. The ground state is therefore

\[\psi(\mathbf{r}_1,\mathbf{r}_2) = \psi_{100}(\mathbf{r}_1)\psi_{100}(\mathbf{r}_2){1\over \sqrt{2}}\left(\ket{\uparrow\downarrow} - \ket{\downarrow\uparrow}\right).\]

(I’m using a different notation here than in Townsend, with the spatial part written in terms of wavefunctions (position representation) because I find it simpler to write out, see Townsend 12.15 for the equivalent state written out in terms of kets only).

Note that the two-particle wavefunction is normalized such that

\[\int d^3\mathbf{r_1}d^3\mathbf{r_2}\, \psi(\mathbf{r}_1,\mathbf{r}_2) = 1.\]

Now if we treat \(\hat{H}_\mathrm{int}\) as a perturbation, then we can calculate the correction to the ground state energy as

\[E^{(1)}_1 = \braket{\Psi^{(0)}_1|\hat{H}_\mathrm{int}|\Psi^{(0)}_1}\]

\[= \int d^3\mathbf{r_1}d^3\mathbf{r_2}\, \psi^\star_{100}(\mathbf{r}_1)\psi^\star_{100}(\mathbf{r}_2) {e^2\over 4\pi\epsilon_0 |\mathbf{r}_2-\mathbf{r}_1|}\psi_{100}(\mathbf{r}_1)\psi_{100}(\mathbf{r}_2)\]

(since the perturbation doesn’t couple to the spin part of the state, the spin parts of the matrix element can be ignored, they give a factor of unity).

This integral can be evaluated analytically, it’s a bit tricky so I will include that proof separately, but the result is, for \(\psi_{100}\propto e^{-Zr/a_0}\),

\[E^{(1)}_1 = {e^2\over 4\pi\epsilon_0} \left\langle {1\over |\mathbf{r}_2-\mathbf{r}_1|} \right\rangle = {e^2\over 4\pi\epsilon_0} {5Z\over 8a_0}\]

\[= {5\over 8} Z{\alpha \hbar c\over a_0} = {5\over 4}Z{1\over 2}\alpha^2 m_e c^2 = {5\over 2}\times 13.6\ \mathrm{eV} = 34\ \mathrm{eV}.\]

This gives the ground state energy as

\[E_0 = (-108.8+34)\ \mathrm{eV} = -74.8\ \mathrm{eV}.\]

Not too far off the true ionization energy of helium which is \(\approx 79\ \mathrm{eV}\), but it is also not very accurate. We shouldn’t be too surprised by this because the perturbation term in the Hamiltonian is not that small compared to the other terms, so perturbation theory shouldn’t be expected to work too well.

Excited states. Now let’s think about the first excited state. This will involve promoting one of the electrons to the \(n=2\) level. In this case where we have different spatial states for each electron, we can construct either symmetric or antisymmetric spatial states

\[\psi_s(\mathbf{r}_1,\mathbf{r}_2) = {1\over \sqrt{2}} \left( \psi_{100}(\mathbf{r}_1)\psi_{2\ell m}(\mathbf{r}_2) + \psi_{2\ell m}(\mathbf{r}_1)\psi_{100}(\mathbf{r}_2)\right)\]

\[\psi_a(\mathbf{r}_1,\mathbf{r}_2) = {1\over \sqrt{2}} \left( \psi_{100}(\mathbf{r}_1)\psi_{2\ell m}(\mathbf{r}_2) - \psi_{2\ell m}(\mathbf{r}_1)\psi_{100}(\mathbf{r}_2)\right).\]

These need to paired with either antisymmetric or symmetric spin states to make an overall antisymmetric wavefunction. The possible states are therefore the spin singlet state

\[\psi(\mathbf{r}_1,\mathbf{r}_2) = {1\over \sqrt{2}} \psi_s(\mathbf{r}_1,\mathbf{r}_2)\left(\ket{\uparrow\downarrow} - \ket{\downarrow\uparrow}\right)\]

or the triplet states

\[\begin{split}\psi(\mathbf{r}_1,\mathbf{r}_2) = \psi_a(\mathbf{r}_1,\mathbf{r}_2)\times \begin{cases} \ket{\uparrow\uparrow}\\ {1\over \sqrt{2}} \left(\ket{\uparrow\downarrow} + \ket{\downarrow\uparrow}\right)\\ \ket{\downarrow\downarrow} \end{cases}.\end{split}\]

With the four possible combinations \((\ell, m) = (0,0), (1,-1), (1,0), (1,1)\) and the four possible spin states (one singlet, three triplet), we end up with 16 possible wavefunctions.

The wavefunctions \(\psi_s\) and \(\psi_a\) have an important difference: the antisymmetric wavefunction \(\psi_a\) vanishes when \(\mathbf{r}_1=\mathbf{r}_2\), the symmetric one does not. In the antisymmetric state, the two electrons avoid each other. This is sometimes described as an exchange interaction or exchange force that keeps the particles apart. It is a purely quantum mechanical effect that arises directly from the need to have an antisymmetric state for fermions.

This difference has a direct impact on the energies of the singlet vs triplet states. The first order correction to the energy of the triplet states is

\[\Delta E = {1\over 2}\int d^3\mathbf{r_1} d^3\mathbf{r}_2\ \psi^\ast_{100}(\mathbf{r}_1)\psi^\ast_{2\ell m}(\mathbf{r}_2){e^2\over 4\pi\epsilon_0|\mathbf{r_2}-\mathbf{r_1}|}\psi_{100}(\mathbf{r}_1)\psi_{2\ell m}(\mathbf{r}_2)\]

\[+ {1\over 2}\int d^3\mathbf{r_1} d^3\mathbf{r}_2\ \psi^\ast_{100}(\mathbf{r}_1)\psi^\ast_{2\ell m}(\mathbf{r}_2){e^2\over 4\pi\epsilon_0|\mathbf{r_2}-\mathbf{r_1}|}\psi_{2\ell m}(\mathbf{r}_1)\psi_{100}(\mathbf{r}_2)\]

\[+ {1\over 2}\int d^3\mathbf{r_1} d^3\mathbf{r}_2\ \psi^\ast_{2\ell m}(\mathbf{r}_1)\psi^\ast_{100}(\mathbf{r}_2){e^2\over 4\pi\epsilon_0|\mathbf{r_2}-\mathbf{r_1}|}\psi_{100}(\mathbf{r}_1)\psi_{2\ell m}(\mathbf{r}_2)\]

\[+ {1\over 2}\int d^3\mathbf{r_1} d^3\mathbf{r}_2\ \psi^\ast_{2\ell m}(\mathbf{r}_1)\psi^\ast_{100}(\mathbf{r}_2){e^2\over 4\pi\epsilon_0|\mathbf{r_2}-\mathbf{r_1}|}\psi_{2\ell m}(\mathbf{r}_1)\psi_{100}(\mathbf{r}_2)\]

We can write this as \(\Delta E = J + K\) with

\[ J = \int d^3\mathbf{r_1} d^3\mathbf{r}_2\ |\psi_{100}(\mathbf{r}_1)|^2 |\psi_{2\ell m}(\mathbf{r}_2)|^2{e^2\over 4\pi\epsilon_0|\mathbf{r_2}-\mathbf{r_1}|}\]

and

\[K = \int d^3\mathbf{r_1}\int d^3\mathbf{r}_2\ \psi^\ast_{100}(\mathbf{r}_1)\psi^\ast_{2\ell m}(\mathbf{r}_2){e^2\over 4\pi\epsilon_0|\mathbf{r_2}-\mathbf{r_1}|}\psi_{2\ell m}(\mathbf{r}_1)\psi_{100}(\mathbf{r}_2).\]

Question

The integral \(J\) has a simple physical interpretation: what is it?

If we instead used \(\psi_a\), corresponding to the spin triplet state, we would find the energy shift is \(\Delta E = J - K\). The spin triplet state has a lower energy than the spin singlet state, even though there is no spin term in the Hamiltonian! The symmetry of the spin state introduces (anti) correlations in the positions of the two electrons. When the spin state is symmetric, the spatial wavefunction is antisymmetric, giving a low probability that the electrons will be found close together. This leads to less repulsion between the electrons, lowering the overall energy.

Here is an energy level diagram for helium, taken from Sakurai and Napolitano. The terms para and ortho helium refer to whether the electrons are in a spin singlet or triplet state respectively.

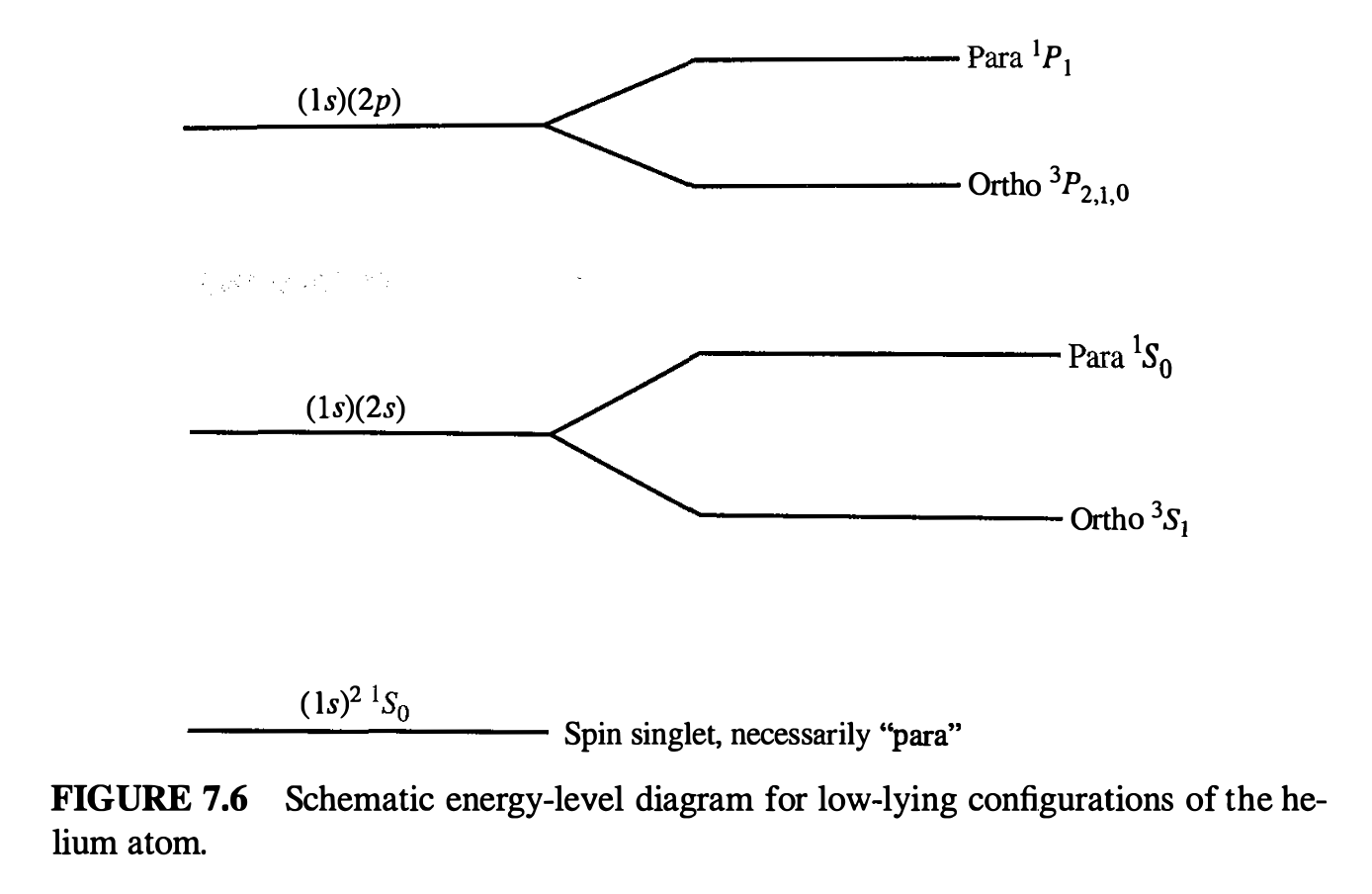
Question:

Look carefully at the diagram. Does it make sense given what we have discussed? What do the labels for each level mean?

Notice that the overall shift depends on the choice of \(\ell\) for the second electron, but not on \(m\) – can you see why looking at the integrals?

Count the number of states at each level. Does it make sense?

Further reading

• Townsend Chapter 12.2 covers the helium atom.